问题解决过程视域下小学生计算思维评价量表的开发与验证

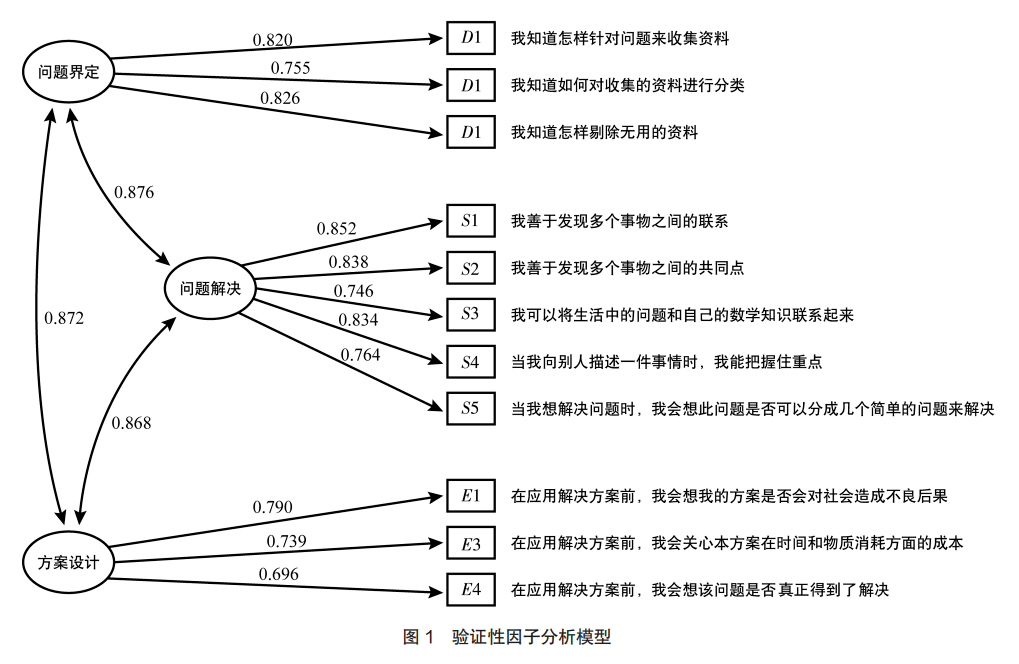
基于综合技能的计算思维评价是近几年跨学科教学背景下计算思维研究发展的新趋势，即计算思维评价不再与具体的编程知识结合，而是泛化为具体的能力集合。这种评价视角使得计算思维评价方式更具迁移性，顺应了当前计算思维融入其他非计算机学科的教学趋势，具体形式主要是通过量表评价。这些量表主要参考了国际教育技术学会 (International Society for Technology in Education，简称 ISTE)构建的基础教育阶段计算机科学学习能力的能力框架，包含了创造力、算法思维、批判性思维、问题解决能力、合作能力、沟通技能六个方面 [6]。国外研究者基于该框架设计了针对大学生的计算思维五因子量表 [7]。在此基础上，白雪梅等 [8]将该量表进行了汉化，保留了该量表的五因子结构，针对我国的高中生群体进行了适当改编，并测量了我国高一、高二学生的计算思维。张屹等 [9]基于 ISTE的框架，设计了面向小学生的计算思维量表，并测评了三年级和五年级学生的计算思维。这些量表在概念倾向上认为计算思维是由一系列思维技能组成的，因而测量内容多是对综合技能的测量。

在计算思维领域中，较多的研究者更倾向于计算思维是由一系列以问题解决为导向的思维过程组成的。这些思维过程包含了抽象、算法设计、自动化、数据分析、数据表征、分解、模式识别、仿真、调试、评价等。陈兴冶等人 [10]进行了初步的尝试，建立了计算思维评价指标体系，将计算思维技能划分为分解、抽象、概括、算法、评估，体现了计算思维的过程评价。但该量表是基于高中信息技术课程标准开发的，因而包含算法的设计、测试、评价等文字描述内容，难以进行跨学科应用。

综上所述，尽管目前国内外研究者已经开发了一些计算思维评价量表，但是当前的量表更多地关注评价计算思维发展的技能结果，较少评价计算思维发展的思维过程。因此，设计面向计算思维过程评价的量表，不仅能够更好地满足小学生计算思维过程发展的评价需求，也能够为计算思维与跨学科教育教学融合的多样化评价提供更多工具选择。

二、 理论框架

来自瑞士联邦理工学院的学者莫甘娜·奈特（ Morgane Knight）等 [11]从问题解决的角度界定了计算思维，构建了计算问题解决模型，其中包含问题界定、形成想法、制定机器人的行为、编写程序、方案评价几个过程。本研究基于该计算问题解决模型，进一步将 “形成想法、制定机器人的行为、编写程序 ”概括为 “问题解决 ”，最终形成 “问题界定 ”“问题解决 ”和 “方案评价 ”三维计算思维框架，使其更适应跨学科及非编程课程的计算思维过程发展评价。其三维方面具体描述如下：

（一）问题界定

问题界定是计算思维发展的基础环节。“问题”可以被定义为任何混淆人类思维、有挑战性的、模糊不清的东西，而问题解决的第一步就是问题界定。问题界定指的是学习者以符号、图像或言语等形式抽象提取出关键问题信息的过程。对于学习者的计算思维发展而言，学习者能够清晰认识自己所面临的问题并提取出有效信息至关重要，由此可以看出评价学习者问题界定的关键在于评价学习者对问题信息进行抽象的能力。学习者对问题信息进行抽象的思维过程是评价其计算思维发展的重要指标。周以真 [12]明确提出，计算思维的基础就是判断关键环节和次要环节的过程。因此，在问题界定中，判断学习者是否能够有效识别问题信息、能够把握问题本质，可以有效地评价其计算思维的发展水平。

（二）问题解决

问题解决是计算思维发展的核心环节，是计算思维的重要组成部分。学习者应用计算思维的最终目的就是解决问题。因此，学习者能够思路清晰地设计问题解决方案是评价其计算思维发展水平的重要指标。如在编程任务中，学习者需要设计算法让计算机自动化地解决问题，这些算法实际上就是解决问题的步骤 [4]。由于本研究中所提出的框架更关注在非编程学科中评价计算思维，因此将算法设计泛化为涉及特定策略的方案设计。这一观点也得到了研究者的支持 [13]。即在评价计算思维问题解决这一环节时，不应该局限于使用特定的技术，而是更具有广泛性。

（三）方案评价

方案评价是计算思维发展的重要环节，也是计算思维中重要的思维过程。学习者在应用计算思维解决问题时，需要对问题解决的方案和问题解决的结果进行分析与判断，并根据分析的结果修改方案。因此，对问题解决方案的效率、影响、优缺点进行分析是评价计算思维发展水平的有效指标。在计算机学科中，解决问题的方案对应的是设计的算法，评价的内容关注的是时间、效率和存储等；在非计算机的领域中，解决问题的方案并不指具体的算法，而是一个个解决问题的步骤，此时对方案的评价意味着评价问题解决方案的效率、资源（如物力、人力、财力）的使用等 [14]。例如，有研究者在对学生的计算思维考察中，就非常重视学生在评价效率和资源利用方面的能力，以及识别和评估结果的能力 [13]。因此，判断学生是否能够对问题解决方案的效率、影响、优缺点进行合理分析可以有效地评价其计算思维的发展水平。

三、 研究方法

（一）研究对象

本研究中采取方便抽样的方法，面向小学三年级到六年级的 229名学生发放了问卷，一共收回 203份有效问卷，其中，男生 112人（ 55.2%），女生 91人（ 44.8%）， 140人（ 69.0%）有过编程学习的经验， 63人（ 31.0%）没有学习过编程。参与调查的学生主要来自西南地区的学校，其中，三年级 11人（ 5.4%），四年级 54人（ 26.6%），五年级 134人（ 66.0%），六年级 4人（ 2.0%）。本研究在量表验证部分使用了所有年级的数据，由于部分年级样本数量较少，不具有代表性，因此在量表应用部分仅分析四、五年级共计 188名学生数据。

（二）研究工具

本研究设计的问卷包含两个部分：第一个部分是对人口统计学信息的调查，包含性别、年级、地区以及是否学习过计算机编程；第二个部分是计算思维测量量表，设计了包含问题界定（例如“当我遇到问题时，我会思考此问题是否有可能解决”）、问题解决（例如“当我做事情前，我会制订一个清晰的计划”）、方案评价（例如“在应用解决方案后，我会想该问题是否得到了真正的解决”）三因子结构的计算思维量表。其中，问题界定与方案评价依据概念定义进行相应题项设计，问题解决这一维度的题项设计参考了经典的“问题解决量表”，该量表自 1982年被提出后受到研究者的广泛应用 [15]。初始量表包含以李克特五点量表测得的 25个问题。

（三）数据处理与分析

使用开源统计分析工具 jamovi将样本随机分为了两个子样本，并且使得两个样本中学生的年级分布大致相似。其中，样本一共计 109人，用于探索性因子分析；样本二共计 94人，用于验证性因子分析。其他数据分析均使用到样本总体。

四、 研究结果

（一）量表的验证

（ 1）探索性因子分析

本研究使用 jamovi对样本一（ n=109）的数据进行了主成分分析，选择斜交旋转法进行旋转。结果显示： KMO=0.909，巴特利特（ Bartlett's）球形检验 χ2(300)=2014， p＜ 0.001。 KMO≥0.8，说明各变量适合进行因子分析，且巴特利特球形检验结果达到了显著水平，也说明各个变量适合进行因子分析。对数据进行探索性因子分析后，以因子载荷大于 0.4且不存在交叉载荷为标准，删去了 3个测量题项。

本研究对修订后的计算思维量表再次进行了探索性因子分析。结果显示： KMO=0.904，巴特利特球形检验 χ2(231)=1 772， p＜ 0.001，适合进行探索性因子分析。选取主轴法进行因子提取，使用斜交旋转法进行旋转。对于各项目的取舍，以因子载荷大于 0.4，独特剩余值小于 0.6，且不存在交叉载荷为标准，删去了 7个测量题项，剩余 15个测量指标。然后抽取出来三个因子，分别是：问题界定、问题解决和方案评价，累积解释了总变异的 64.2%。各因子的解释率分别为：问题界定 15.6%，问题解决 31.4%，方案评价 17.2%。

（ 2）验证性因子分析

使用 jamovi软件对第二个样本 ( n =94) 数据进行了验证性因子分析。在分析过程中根据标准载荷系数值对模型进行修正，最终确定了 11个测量指标。图 1展示了验证性因子分析的结果。在检验模型的拟合程度时参照了以下拟合指标： χ2/ df ＜ 3， TLI＞ 0.9， CFI＞ 0.9， SRMR≤0.05， RMSEA≤0.1。结果显示： χ2=74.6， df=41， χ2/ df = 1.8195 ， TLI=0.933， CFI=0.950， SRMR=0.0401， RMSEA=0.0934，说明计算思维的三维理论模型与数据的拟合程度较好。

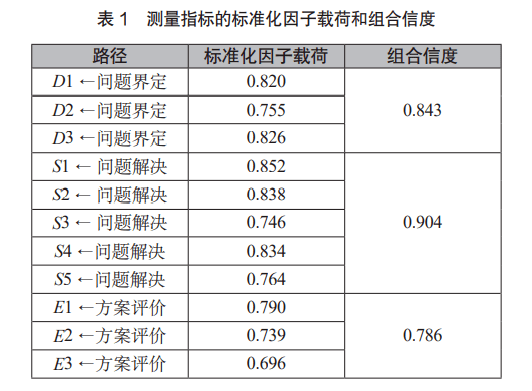
（ 3）效度检验

①聚敛效度

本研究进一步对模型进行了聚敛效度分析，分析了各个测量指标的标准化因子载荷并计算了三个因子的组合信度。组合信度表示测量指标之间的关联度，较高的组合信度意味着测量指标具有更好的同构性，一般要求该数值在 0.6以上。各个因子的组合信度值可以根据测量指标的标准化因子载荷值及测量指标的误差方差计算得到。

结果如表 1所示。该模型中测量指标的标准化因子载荷取值在 0.688～ 0.848，这代表这些测量指标均具有较好的聚敛效度，可以有效反映对应的因子。各因子的组合信度分别为：问题界定 (0.843)、问题解决 (0.904)、方案评价 (0.786)。三个因子的组合信度值都高于 0.7，表示所有因子的测量题目具有较好的关联度与同构性。

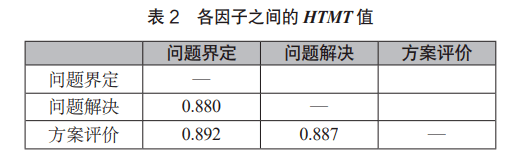
②区分效度

本研究使用了异质—单质比率（ Heterotrait—monotrait Ratio，简称 HTMT）方法来计算量表的区分效度。该方法使用特质间相关与特质内相关的比率来表征区分效度，该比率的数值越小，则区分效度越好。如果 HTMT的值大于 0.85或 0.90，则表明区分效度不好。

结果如表 2所示，问题界定与问题解决两个因子的 HTMT值为 0.880，问题界定与方案评价两个因子的 HTMT值为 0.892，问题解决与方案评价两个因子的 HTMT值为 0.887，均在可接受的范围内，量表的区分效度较好。

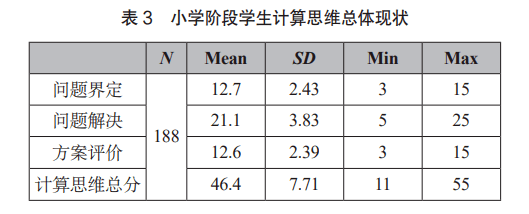
（ 4）信度检验

本研究采用克伦巴赫系数检测量表的信度，并参照标准：假设，表示量表的信度良好；假设，表示量表的信度可以接受。分析结果显示：计算思维量表的总信度是 0.869，问题界定、问题解决及评价的克伦巴赫系数依次是 0.795、 0.839、 0.820，均高于 0.70，这说明计算思维量表中三个因子具有较好的内部一致性。

（二）量表的应用

（ 1）小学生计算思维总体现状

本研究对小学生的计算思维得分进行了描述性统计，计算了学生在计算思维三个维度上的均值、标准差、最小值和最大值，以分析学生的计算思维现状，数据结果如表 3所示。计算思维量表的满分总分是 55分，学生样本得分的均值是 46.4分，占满分值的 84.4%，这说明小学阶段学生的计算思维还是有一定提升空间的。同时，绝大多数的学生分数都处于 40～ 55的区间，可见小学生计算思维的总体水平是较好的。

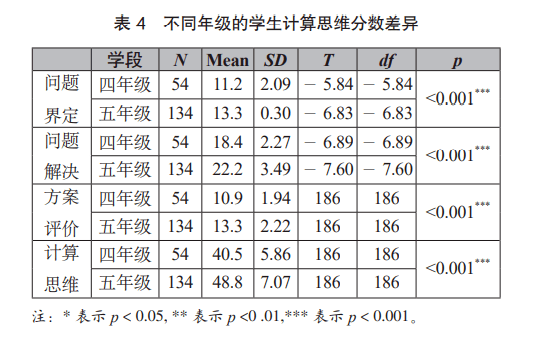
（ 2）小学生计算思维差异分析

①不同年级学生的计算思维差异

本研究使用独立样本 T检验的方法，检验了两个年级的学生在计算思维上的差异，结果如表 4所示。研究发现：在计算思维总分上，各年级存在显著性差异（ T=－ 7.60， p=0.000），并且在问题界定（ T=－ 5.84， p=0.000），问题解决（ T=－ 6.83， p=0.000），方案评价（ T=－ 6.89， p=0.165）几个维度上，两个年级都存在 p＜ 0.001显著性的差异。

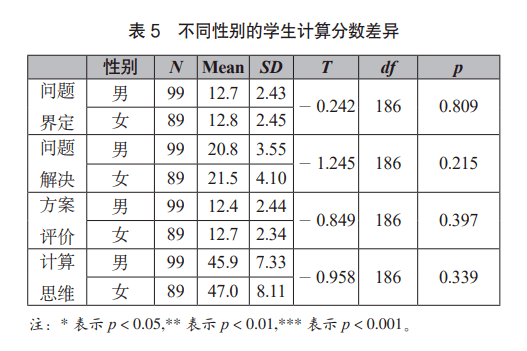
②不同性别学生的计算思维差异

本研究使用了独立样本 T检验的方法，检验了不同性别的学生在计算思维上的差异，结果如表 5所示。研究发现：在计算思维总分上，男女不存在显著性差异（ T=－ 0.958， p=0.339），并且在问题界定（ T=－ 0.242， p=0.809）、问题解决（ T=－ 1.245， p=0.215）、方案评价（ T=－ 0.849， p=0.397）三个维度上，男女都没有显著性的差异。

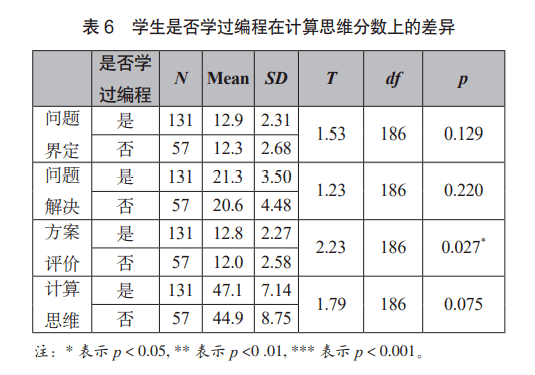
③是否有编程学习经验的学生在计算思维上的差异

研究使用独立样本 T检验的方法，对比了学过编程与没有学过编程的学生在计算思维量表得分上的差异，结果如表 6所示。研究发现，学过编程的学生在方案评价上显著高于没有学过编程的学生（ T=2.23， p=0.027）。在计算思维总分（ T=1.79， p=0.075）以及问题界定（ T=1.53， p=0.129）和问题解决（ T=1.23， p=0.220）两个维度上，并没有统计学意义上的显著差异，但是有编程学习经历的学生也高于没有编程经历的学生。

五、讨论与分析

本研究中最终形成的量表为李克特五点式量表，具有三因子结构，由 11个项目组成，其中包括问题界定（ 3个）、问题解决（ 5个）、方案评价（ 3个）。因子分析、聚敛效度、区分效度以及信度检验的结果都保证了该量表的有效性。在因子分析方面，进行探索性因子分析时，由于部分指标的因子载荷较低，删去了一些测量指标。例如 “在没有证据前，我不相信直觉 ”，该测量指标属于问题解决的维度，分析该题项因子载荷较小的原因，可能是青少年在日常学习中很少体验到给出证据来论证观点或者假设的学习过程，因此会对 “证据 ”一词感到陌生，在理解该测量指标上遇到困难。在探索性因子分析之后，进行了验证性的因子分析来验证三因子结构的模型与数据是否有较好的拟合度。在考察测量数据与计算思维量表三因子结构模型的拟合程度时，本研究使用了绝对拟合指数和增量拟合指数对模型卡方统计量进行了补充 [16]。验证性因子分析的结果充分说明了该量表具有较好的结构效度。在区分效度方面，该量表的 3个因子两两之间的 HTMT值均 ≤0.9，其中问题解决与方案评价的 HTMT值刚好等于 0.9，说明问题解决与方案评价这两个因子的区分效度是稍有不足的。这可能是因为在应用计算思维的过程中，问题解决与方案评价的这两种思维过程通常是接连发生的，学习者会在解决问题的过程中不断地评价方案，因此在评价这两种思维过程时，不能很好地将两个因子区分开。但其 HTMT值仍然是在可接受范围内的，量表整体的区分效度是较好的。

使用该量表调查小学生计算思维水平现状，主要得出了三点结论：第一，在小学阶段计算思维随着年级的增长而提升。本研究中四、五年级学生在计算思维得分上存在显著差异，并且在计算思维以及其各个维度上，五年级学生都显著高于四年级。一些相关研究也有类似发现，如郁晓华等人 [17]的研究中将学生的计算机发展水平为划分幼儿园至二年级、三至五年级、六至八年级和九至十二年级 4个阶段，并发现六至八年级学生的计算思维发展水平较三至五年级学生更高。第二，小学生的计算思维在性别上没有显著性差异。这与一些相关研究的发现是存在共性的。国外研究者发现在小学阶段，不同性别的学生在计算思维发展上并没有显著的差异，但是在初高中阶段，性别的差异会凸显出来 [18]。我国研究者也有类似发现，张屹等 [10]发现我国小学生中男女的计算思维不存在差异，白雪梅等 [9]发现我国高中生群体中男生的计算思维显著高于女生。研究者指出应当在小学阶段加强对学习者计算思维的培养，因为在这个阶段性别的差异是比较容易去弥补的，这对于缩小未来不同性别的计算思维水平差异至关重要。第三，有编程学习经验的小学生具备更强的方案评价能力，但是在其他计算思维维度上与没有编程学习经验的小学生相比没有显著差异。由此可见，尽管近年来国家非常重视编程教育的推广，但是小学阶段以编程为媒介的计算思维教学效果还有提升空间。基于以上发现和讨论，本研究针对小学的计算思维教学提出了以下三点建议：

第一，结合不同年龄段的认知特点采取多元的计算思维教学方式。研究者指出结合认知发展阶段来制定适合不同年级的计算思维课程是至关重要的。在具体实施上，依据皮亚杰认知发展理论，低年级的学习者（具体运算阶段）主要依靠他们的感知来解决问题，这一时期学生开始具有抽象的概念，但是思维活动仍需具体活动或实体材料的支持，因此可以通过卡片、拼图等教具来辅助培养学生的计算思维，让学习者在具体的活动中通过与实体工具的交互发展计算思维；而高年级的学习者（形式运算阶段）已经超越对实体事物的依赖，具备处理抽象概念和假设推演的能力，因此针对这个学段可以依托图形化编程工具来学习更为抽象、复杂的计算思维。

第二，以问题解决为导向，将计算思维教学融入其他学科教学中。研究者已经达成共识，计算思维不仅可以应用于计算机科学的领域，也可以应用到数学、科学、英语和文学等学科中。近年来，国内外的研究者都尝试将计算思维融入学科教育中。将计算思维教学与其他学科教学融合，不仅能够让学生认识到计算思维并不局限于编程这一种形式，不局限于计算机科学这一领域，而是作为一项重要的思维能力可以帮助他们解决各个领域中的问题，同时还可以促进他们对于学科知识的深入理解。

第三，对学生应用计算思维解决问题的思维过程开展评价。评价是计算思维教学中的重要环节，在小学阶段，对计算思维的评价不应局限于对计算思维概念或者是对编程技能的考核，而应该加强对学生思维过程的重视。本研究中提出的理论框架从问题解决过程的视角界定了计算思维的关键思维过程，并基于该理论框架开发了量表。在未来，教育工作者可以基于该理论框架开发其他形式的评价工具，从而帮助教师评价学生计算思维的思维过程，提升计算思维的教学质量。

参考文献 ：

[1]林泽珊，魏轶娜，赵腾任 .基于 TPACK的中小学信息技术教师计算思维教学能力现状调查 [J].数字教育， 2021， 7(6)： 70-76.

[2]李阳 .计算思维导向的跨学科儿童编程教育模式研究：基于芬兰儿童编程教育的经验与启示 [J].现代教育技术， 2020， 30(6)： 19-25.

[3]TANG X,YIN Y,LIN Q,et al.Assessing computational thinking:a systematic review of empirical studies[J]. Computers & education,2020,148(4):103798.

[4]BARR V,STEPHENSON C.Bringing computational thinking to K-12[J].Acm Inroads,2011,2(1):48.

[5]刘敏娜，张倩苇 .国外计算思维教育研究进展 [J].开放教育研究， 2018(1)： 41-53.

[6]CSTA ISTE.Operational definition of computational thinking for k12 education[EB/OL].[2022-09-03].http://csta.acm.org/Curriculum/sub/CurrFiles/471.1.CTLeadershiptToolkit-sp-vF.pd.

[7]KORKMAZ O,CAKIR R,OZDEN M Y.A validity and reliability study of the computational thinking scales (cts)[J].Computers in hu-man behavior,2017,72(7)： 558-569.

[8]白雪梅，顾小清 .K12阶段学生计算思维评价工具构建与应用 [J].中国电化教育， 2019(10)： 83-90.

[9]张屹，莫尉，张岩，等 .我国小学生计算思维量表研发与应用 [J].中国电化教育， 2020(10)： 49-57.

[10]陈兴冶，马颖莹 .本土化计算思维评价指标体系的构建与探索：基于 1410名高中生的样本分析与验证 [J].远程教育杂志， 2020(5)： 70-80.

[11]CHEVALIER M,GIANG C,PIATTI A,et al.Fostering computational Thinking through Educational Robotics:a model for creative computational Problem Solving[J]. International journal of STEM Education,2020,7(1):58-63.

[12]WING J M.Computational thinking and thinking about computing [EB/OL].(2016-05-09)[2022-09-03].https://www.docin.com/p-1568020984.html.

[13]HEUREUX J,BOISVERT D,COHEN R,et al.IT problem solving:an implementation of computational thinking in information technology[EB/OL].(2012-10-11)[2022-09-04].https://dl.acm.org/doi/epdf/10.1145/2380552.2380606.

[14]WING J M.Computational Thinkign[J].Communications of the ACM,2006,49(3):33-35.

[15]HEPPNER P P,PETERSEN C H.The development and implications of a personal problem-solving inventory[J].Journal of Counseling Psychology,1982,29(1):66-75.

[16]HU Li tze,BENTLER P M.Cutoff criteria for fit indexes in covariance structure analysis:conventional criteria versus new alternatives[J].Structural equation modeling,1999,6(1)： 1-55.

[17]郁晓华，王美玲，程佳敏，等 . 计算思维评价的新途径：微认证 [J]. 开放教育研究， 2022， 28(1)： 107-120.

[18]LUO F,ANTONENKO P D,DAVIS E C.Exploring the evolution of two girls’conceptions and practices in computational thinking in science[J]. Computers & education,2020,146(3):103759.

作者简介：

傅骞（ 1978— ），男，浙江金华人，教授、博士生导师，研究方向为创客教育、创新人才培养；

胡婉青（ 1998— ），女，重庆市人，硕士研究生，研究方向为计算思维、协作学习；

吕巾娇（ 1981— ），女，山西文水人，博士，助理研究员，研究方向为教育技术基础理论、教学设计；

郑娅峰（ 1979— ），女，河南洛阳人，教授、硕士生导师，研究方向为教育数据挖掘、数据可视化，系本文通信作者。

喜欢就点个赞吧 ！返回搜狐，查看更多